definition
kernel density estimation (KDE) is a non-parametric way to estimate the probability density function of a random variable. Kernel density estimation is a fundamental data smoothing problem where inferences about the population are made, based on a finite data sample. In some fields such as signal processing and econometrics it is also termed the Parzen–Rosenblatt window method, after Emanuel Parzen and Murray Rosenblatt, who are usually credited with independently creating it in its current form.[1][2] One of the famous applications of kernel density estimation is in estimating the class-conditional marginal densities of data when using a naive Bayes classifier,[3][4] which can improve its prediction accuracy.[3]

where K is the kernel — a non-negative function — and h > 0 is a smoothing parameter called the bandwidth. A kernel with subscript h is called the scaled kernel and defined as Kh(x) = 1/h K(x/h). Intuitively one wants to choose h as small as the data will allow; however, there is always a trade-off between the bias of the estimator and its variance. The choice of bandwidth is discussed in more detail below.
How to calculate KDE faster? With KD tree.
find maximum in KDE
mean-shift: using the mean of window in the selected aread, and with kernel function. To find the local maximum.
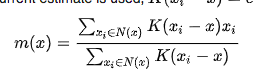
summay
To fetch a distribution from samples, we can use paramter model estimation & non-paramter model estimation. For the param model, we have generative model(MLE) & discriminative model(MAP).
KDE is a kind of the non-parameter model, if we could find the model is not easy for use to construct the model.
Ref:
