definition
Gradient descent is a first-order iterative optimization algorithm for finding a local minimum of a differentiable function. The idea is to take repeated steps in the opposite direction of the gradient (or approximate gradient) of the function at the current point, because this is the direction of steepest descent. Conversely, stepping in the direction of the gradient will lead to a local maximum of that function; the procedure is then known as gradient ascent.
In optimization, if the function is convex, there is closed form solution. Like least square solution. But for some complex non-convex function, to find the potenail max/min state, we must use some iterative methods.
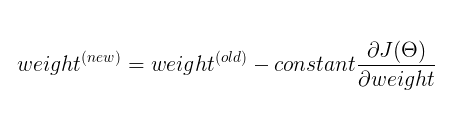
type
Momentum Based Gradient Descent
In order to avoid drawbacks of vanilla Gradient Descent, we introduced momentum based Gradient Descent where the goal is to lower the computation time and that can be achieved when we introduce the concept of experience i.e. the confidence using previous steps.
Nesterov Accelerated Gradient Descent(NAG)
Nesterov accelerated Gradient(NAG) is a way to provide history to our momentum.

Other GD methods like: Adam, RMSprop, Adadelta, AdaGrad. See ref 3.
strategy
- Stochastic Gradient Descent. Shuffle training data & partition training data into m examples. Adv: easy; efficient; but noisy.
- Batch gradient descent: sum all. Less noisy; produce stable convergence. Compuational high.
- Mini-batch: easy to fit; stable.
Ref:
