Practice makes perfect.
Basic Algorithm
Sort
// Quick Select
void QuickSort(const int l, const int r, std::vector<int>& arr) {
if (l >= r) return;
int num = arr[l + (r - l)/2];
int i = l - 1;
int j = r + 1;
while (i < j) {
do {
++i;
} while (arr[i] < num);
do {
--j;
} while (arr[j] > num);
if (i < j)
std::swap(arr[i], arr[j]);
}
QuickSort(arr, l, j);
QuickSort(arr, j+1, r);
}
int CalculateKthLargestNumber(const int l, const int r,
const int k, std::vector<int>& nums) {
if (l >= r) return nums[l];
int i = l - 1;
int j = r + 1;
const int mid = nums[l + (r - l)/2];
while (i < j) {
do {
++i;
} while (nums[i] < mid);
do {
--j;
} while (nums[j] > mid);
if (i < j) {
std::swap(nums[i], nums[j]);
}
}
return j + 1 >= k ? CalculateKthLargestNumber(l, j, k, nums) :
CalculateKthLargestNumber(j+1, r, k, nums);
}
// Merge Sort
void MergeSort(const int l, const int r, std::vector<int>& nums) {
if (l >= r) return;
const int mid = l + (r - l)/2;
MergeSort(l, mid, nums);
MergeSort(mid+1, r, nums);
std::vector<int> tmp(r - l + 1);
int i = l;
int j = mid+1;
int cnt = 0;
while (i <= mid && j <= r) {
if (nums[i] <= nums[j]) {
tmp[cnt++] = nums[i++];
} else {
tmp[cnt++] = nums[j++];
}
}
while (i <= mid) tmp[cnt++] = nums[i++];
while (j <= r) tmp[cnt++] = nums[j++];
for (int i = l, j = 0; i <= r; ++i, ++j) {
nums[i] = tmp[j];
}
}
Binary Search
// Binary Search(Int)
int BinarySearch(vector<int>& nums, int target) {
int stt_idx = 0;
int fin_idx = nums.size() - 1;
int mid_idx;
while (stt_idx + 1 < fin_idx) {
mid_idx = stt_idx + (fin_idx - stt_idx)/2;
if (nums[mid_idx] < target) stt_idx = mid_idx;
else if (nums[mid_idx] >= target) fin_idx = mid_idx;
}
if (nums[stt_idx] == target) return stt_idx;
if (nums[fin_idx] == target) return fin_idx;
return -1;
}
// Binary Search(Double)
bool Check(const double x) { /*....*/ }
double BinarySearch(vector<int>& nums, int target) {
const double eps = 1.0e-6;
double l = min_val;
double r = max_val;
while (r - l > eps) {
const double mid = (l + r) / 2.0;
if (Check(mid)) r = mid;
else l = mid;
}
return l;
}
Large Value Operation
// Store number smalle from 0 index.
// Add
std::vector<int> Add(std::vector<int> &A, std::vector<int> &B) {
if (A.size() < B.size()) return Add(B, A);
std::vector<int> C;
int t = 0;
for (int i = 0; i < A.size(); ++i) {
t += A[i];
if (i < B.size()) t += B[i];
C.push_back(t % 10);
t /= 10;
}
if (t) C.push_back(t);
return C;
}
// Minus, A >= B >= 0.
std::vector<int> Sub(std::vector<int> &A, std::vector<int> &B) {
vector<int> C;
for (int i = 0, t = 0; i < A.size(); ++i){
t = A[i] - t;
if (i < B.size()) t -= B[i];
C.push_back((t + 10) % 10);
if (t < 0) t = 1;
else t = 0;
}
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
// Multiple
std::vector<int> Mul(std::vector<int> &A, int b) {
std::vector<int> C;
int t = 0;
for (int i = 0; i < A.size() || t; ++i) {
if (i < A.size()) t += A[i] * b;
C.push_back(t % 10);
t /= 10;
}
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
// Divide
std::vector<int> Div(std::vector<int> &A, int b, int &r) {
std::vector<int> C;
r = 0;
for (int i = A.size() - 1; i >= 0; --i) {
r = r * 10 + A[i];
C.push_back(r / b);
r %= b;
}
std::reverse(C.begin(), C.end());
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
Prefix Sum
// One dimension prefix sum
S[i] = a[1] + a[2] + ... + a[i]
a[l:r] = S[r] - S[l-1]
// Two dimension prefix sum
S[i, j] = a[1, 1] --- a[1, j]
| |
a[i, 1] --- a[i, j]
Sum of (x1, y1) to (x2, y2)
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]
// 1906. Minimum Absolute Difference Queries
int record[100001][101];
vector<int> minDifference(vector<int>& nums, vector<vector<int>>& queries) {
for (int i = 0; i < nums.size(); ++i) {
for (int j = 1; j <= 100; ++j) {
record[i+1][j] = record[i][j] + (nums[i] == j);
}
}
vector<int> ans;
for (const auto& query : queries) {
const int left = query[0];
const int right = query[1] + 1;
int t = 101;
int cur_min = 101;
for (int i = 1; i <= 100; ++i) {
if (record[right][i] > record[left][i]) {
if (t <= 100) {
cur_min = min(cur_min, i - t);
}
t = i;
}
}
ans.emplace_back(cur_min > 100?-1:cur_min);
}
return ans;
}
Difference
// Could be used for the interval operation
// One Dimension Difference, add [l, r] with C
// B[l] += c, B[r + 1] -= c
// Given prefix sum A, we can have its difference B
// Ai = B1 + B2 + ... + Bi, B is the difference of A
const int N = 100010;
int n, m;
int a[N], b[N];
void Insert(int l, int r, int c) {
b[l] += c;
b[r + 1] -= c;
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
for (int i = 1; i <= n; i ++ ) insert(i, i, a[i]);
while (m -- ) {
int l, r, c;
scanf("%d%d%d", &l, &r, &c);
insert(l, r, c);
}
for (int i = 1; i <= n; i ++ ) b[i] += b[i - 1];
for (int i = 1; i <= n; i ++ ) printf("%d ", b[i]);
return 0;
}
// Two Dimension Difference
// To Box [(x1, y1),(x2, y2)] all elements add c
// A[i,j] = B[1, 1] --- B[1, j]
// | |
// B[i, 1] --- B[i, j]
// B is the difference matrix.
B[x1, y1] += c, B[x2 + 1, y1] -= c, B[x1, y2 + 1] -= c, B[x2 + 1, y2 + 1] += c
Two Pointer
// Longest unrepeated substring
for (int i = 0, j = 0; i < n; ++i) {
while (j < i&& Check(i, j)) ++j;
res = /*.....*/
}
Bit Operation
// kth bit in number.
n >> k & 1
// get last bit one
lowbit(n) = n & ~n;
Discrete
// Discrete the large range
// repeat elements
std::vector<int> alls;
std::sort(std::begin(alls), std::end(alls));
alls.erase(std::unique(std::begin(alls), std::end(alls)), alls.end());
Interval Merge
void Merge(std::vector<std::pair<int, int>>& segs) {
std::vector<std::pair<int, int>> res;
std::sort(begin(segs), end(segs));
int st = -2e9;
int ed = -2e9;
for (const auto& seg : segs) {
if (ed < seg.first) {
if (st != -2e9) res.push_back({st, ed});
st = seg.first;
ed = seg.second;
}
else {
ed = std::max(seg.second, ed);
}
}
if (st != -2e9) {
res.push_back({st, ed});
}
res.swap(segs);
}
Data Structure
Linked List
Adding with Adjecent list.
Stack & Queue
Monotonic stack & queu.
KMP
Trie
Union Find
Heap
Hash
Graph
DFS & BFS
// Tree & Graph store with adjacent matrix M[a][b] (a->b) & adjacent list (a -> b -> c -> d, b, c, d is connected to a)
// DFS
void DFS(const int u, const std::vector<bool>& record) {
record[u] = true;
for (const auto& node : graph[u]) {
if (!record[node]) DFS(node, record);
}
}
// BFS
queue<int> q;
st[1] = true;
q.push(1);
while (q.size()) {
int tp = q.front();
q.pop();
for (const auto& node : graph[tp]) {
if (!st[node]) {
st[node] = true;
q.push(node);
}
}
}
Topological Sort
// Comupation complexity: O(m + n)
// Using indegrees
class Solution {
public:
vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
unordered_map<int, vector<int>> record;
vector<int> indegrees(numCourses, 0);
for (const auto pre : prerequisites) {
record[pre[1]].push_back(pre[0]);
++indegrees[pre[0]];
}
queue<int> status;
for (int i = 0; i < numCourses; ++i) {
if (!indegrees[i])
status.push(i);
}
vector<int> top_res;
while (!status.empty()) {
const auto it = status.front();
top_res.push_back(it);
status.pop();
for (const auto& ele : record[it]) {
--indegrees[ele];
if (!indegrees[ele]) {
status.push(ele);
}
}
}
return top_res.size() != numCourses ? vector<int>() :top_res;
}
};
Shortest Path
Summary:
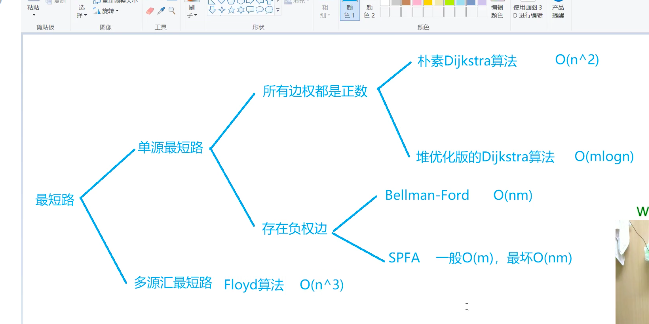
Dijkstra

// Dijkstra, source -> target
// 743. Network Delay Time
class Solution {
public:
struct Node {
int index = -1;
int distance = INT_MAX;
int precurssor = -1;
Node(const int idx, const int dis) {
index = idx;
distance = dis;
}
};
struct Comp {
bool operator()(const struct Node& node1, const struct Node& node2) {
return node1.distance >= node2.distance;
}
};
using InitQueue = priority_queue<Node, vector<Node>, Comp>;
InitQueue InitPriorityQueue(const int N, const int K) {
InitQueue queue;
for (int i = 0; i < N; ++i) {
if (i != K) queue.push(Node(i, INT_MAX));
}
Node start(K, 0);
queue.push(start);
return queue;
}
int networkDelayTime(vector<vector<int>>& times, int N, int K) {
InitQueue Q = InitPriorityQueue(N, K);
unordered_map<int, Node> record;
record.emplace(K, Node(K, 0));
unordered_map<int, vector<vector<int>>> edges;
for (const auto time : times) edges[time[0]].push_back(time);
int longest_dis = -1;
unordered_set<int> visited;
while (!Q.empty()) {
const auto tp = Q.top();
if (tp.distance == INT_MAX) {
if (record.size() < N)
return -1;
else break;
}
Q.pop();
if (visited.find(tp.index) != visited.end()) continue;
for (const auto edge : edges[tp.index]) {
const int new_dis = edge[2] + tp.distance;
if ((record.find(edge[1]) == record.end()) || record.at(edge[1]).distance > new_dis)
{
Node new_node(edge[1], new_dis);
new_node.precurssor = edge[0];
Q.push(new_node);
record.emplace(edge[1], new_node).first->second = new_node;
}
}
visited.insert(tp.index);
}
for (const auto m : record) {
longest_dis = max(m.second.distance, longest_dis);
}
return longest_dis;
}
};
Bellmanford

// 经过k条边适用
SPFA

// 不经过k条边
Floyd
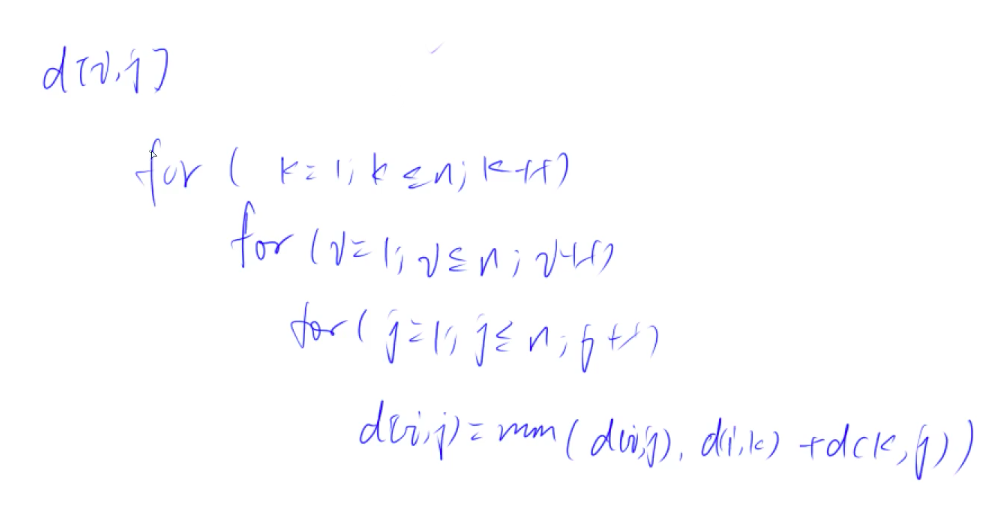
MST
Minimum spanning tree.
Naive Prime:


// Prime
// Kruskal: Union-Find with edge sort.
int n, m; // n是点数,m是边数
int p[N]; // 并查集的父节点数组
struct Edge // 存储边
{
int a, b, w;
bool operator< (const Edge &W)const
{
return w < W.w;
}
}edges[M];
int find(int x) // 并查集核心操作
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
int kruskal()
{
sort(edges, edges + m);
for (int i = 1; i <= n; i ++ ) p[i] = i; // 初始化并查集
int res = 0, cnt = 0;
for (int i = 0; i < m; i ++ )
{
int a = edges[i].a, b = edges[i].b, w = edges[i].w;
a = find(a), b = find(b);
if (a != b) // 如果两个连通块不连通,则将这两个连通块合并
{
p[a] = b;
res += w;
cnt ++ ;
}
}
if (cnt < n - 1) return INF;
return res;
}
Bipartite Graph
Painting method & Hungarian algorithm.
Math
Prime Number
Divisor
Euler’s Totient Function
Fast Power
Extended Euclidean Algorithm
Chinese Remainder Theorem
中国剩余原理。
Gaussian Elimination
高斯消元。
Combination Count
组合计数。
Principal of Tolerance & Exclusion
容斥原理
Game Theory
博弈论。
DP
DP = state representation(how to represent the state, set + attributes[max, min, count]) + state caculation (how to calculate state, set divide,所有选法)
DP optimization: DP code equal transform

Knapsack
背包问题
完全背包问题:
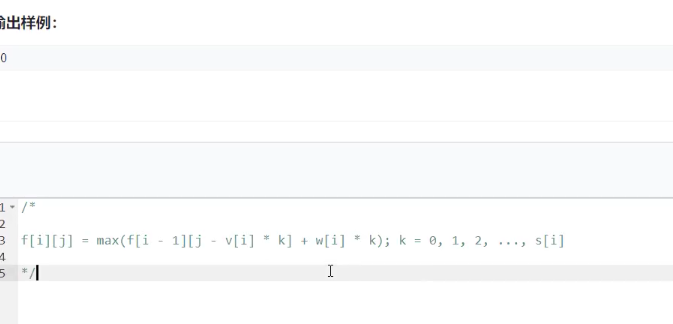
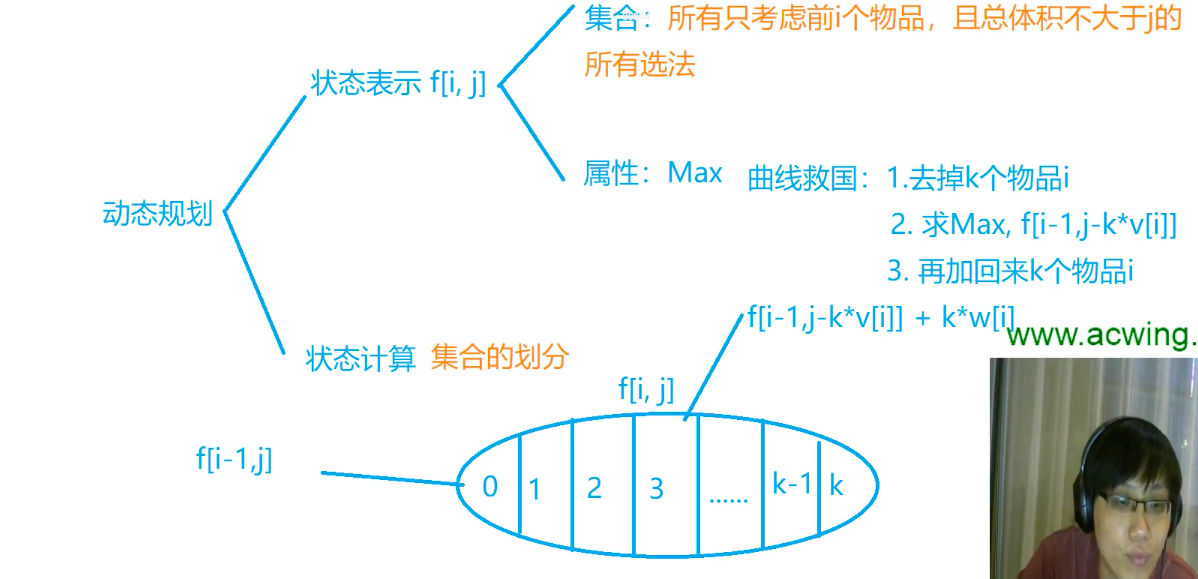

// 0-1 Knapsack: 0-1 背包,每个物体只有1件
// Naive
// f[i, j], previous i objects, volumn <= j, max
// max(f[i-1, j], f[i-1][j-v[i]] + w[i])
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
for (int i = 1; i <= n; i ++ )
for (int j = m; j >= v[i]; j -- ) {
f[i][j] = f[i-1][j];
if (j >= v[i]) f[i][j] = max(f[i][j], f[i-1][j-v[i]] + w[i]);
}
cout << f[n][m] << endl;
return 0;
}
// Optimized
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
for (int i = 1; i <= n; i ++ )
for (int j = m; j >= v[i]; j -- )
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
return 0;
}
// Complete Knapsack: 完全背包,每种物品有无数件
// f[i-1, j - k*v[i]] + k * w[i]
// Naive
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main() {
cin >> n >> m;
for (int i = 1; i <=n; ++i) cin >> v[i] >> w[i];
for (int i = 1; i <= n; ++i)
for (int j = 0; j <= m; ++j)
for (int k = 0; k * v[i] <= j; ++k)
f[i][j] = max(f[i][j], f[i-1][j - v[i]*k] + w[i]*k);
cout << f[n][m] << endl;
return 0;
}
// Optimized
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
for (int i = 1; i <= n; i ++ )
for (int j = v[i]; j <= m; j ++ )
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
return 0;
}
// Multiple Knapsack: 多重背包,每种物品是有限的
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int n, m;
int v[N], w[N], s[N];
int f[N][N];
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i] >> s[i];
for (int i = 1; i <= n; i ++ )
for (int j = 0; j <= m; j ++ )
for (int k = 0; k <= s[i] && k * v[i] <= j; k ++ )
f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);
cout << f[n][m] << endl;
return 0;
}
// Group Knapsack: 分组背包,每组最多一个物品
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int n, m;
int v[N][N], w[N][N], s[N];
int f[N];
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) {
cin >> s[i];
for (int j = 0; j < s[i]; j ++ )
cin >> v[i][j] >> w[i][j];
}
for (int i = 1; i <= n; i ++ )
for (int j = m; j >= 0; j -- )
for (int k = 0; k < s[i]; k ++ )
if (v[i][k] <= j)
f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
cout << f[m] << endl;
return 0;
}
Linear DP
Interval DP
Count DP
计数DP
public int change(int amount, int[] coins) {
int[][] dp = new int[coins.length + 1][amount + 1];
dp[0][0] = 1;
for (int j = 1; j <= coins.length; j++) {
dp[j][0] = 1;
for (int i = 1; i <= amount; i++) {
dp[j][i] = dp[j - 1][i];
if (i - coins[j - 1] >= 0) {
dp[j][i] += dp[j][i - coins[j - 1]];
}
}
}
return dp[coins.length][amount];
}
Digit DP
数位DP
State Compression DP
状态压缩DP。
State Translation DP
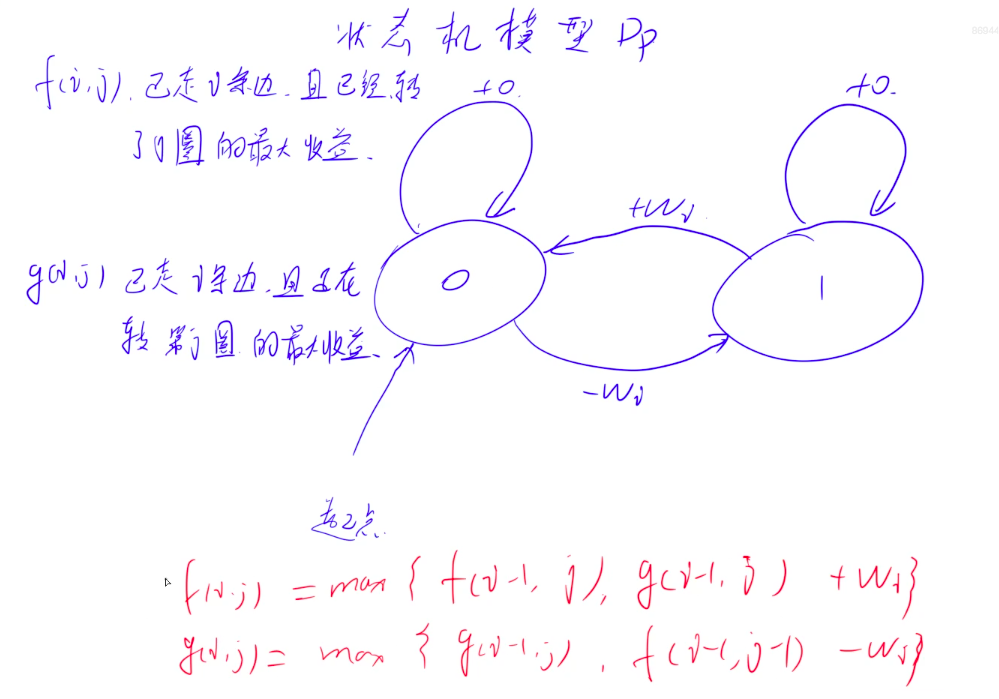
Tree DP
树形DP
Memorial Search
记忆化搜索
Greedy
// Intervals operation
// 56. Merge Intervals
vector<vector<int>> merge(vector<vector<int>>& intervals) {
sort(begin(intervals), end(intervals), [](
vector<int>& v1, vector<int>& v2) {
return v1[0] < v2[0];
});
vector<vector<int>> ans;
int stt = intervals[0][0];
int ed = intervals[0][1];
for (const auto& c : intervals) {
if (c[0] <= ed) {
ed = max(c[1], ed);
stt = min(stt, c[0]);
} else {
ans.push_back(vector<int>({stt, ed}));
ed = c[1];
stt = c[0];
}
}
ans.push_back({stt, ed});
return ans;
}
// 57. Insert Interval
vector<vector<int>> insert(vector<vector<int>>& intervals, vector<int>& newInterval) {
auto low_it = lower_bound(begin(intervals), end(intervals), newInterval, [](
const vector<int>& v1, const vector<int>& v2) {
return v1[1] < v2[0];
});
auto high_it = upper_bound(begin(intervals), end(intervals), newInterval, [](
const vector<int>& v1, const vector<int>& v2) {
return v1[1] < v2[0];
});
if (low_it == high_it) {
intervals.insert(low_it, newInterval);
} else {
--high_it;
(*high_it)[0] = min((*low_it)[0], newInterval[0]);
(*high_it)[1] = max((*high_it)[1], newInterval[1]);
intervals.erase(low_it, high_it);
}
return intervals;
}
// 435. Non-overlapping Intervals
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
if (intervals.empty()) return 0;
sort(begin(intervals), end(intervals), [](const vector<int>& v1,
const vector<int>& v2) {
return v1[1] < v2[1];
});
int res = 0;
int ed = -2e9;
for (const auto& inter : intervals) {
if (ed <= inter[0]) {
++res;
ed = inter[1];
}
}
return intervals.size() - res;
}
// 986. Interval List Intersections
vector<vector<int>> intervalIntersection(vector<vector<int>>& first, vector<vector<int>>& second) {
vector<vector<int>> ans;
int idx1 = 0;
int idx2 = 0;
while (idx1 < first.size() && idx2 < second.size()) {
if (first[idx1][1] < second[idx2][0]) {
++idx1;
} else if (second[idx2][1] < first[idx1][0]) {
++idx2;
} else {
ans.emplace_back(vector<int>({max(first[idx1][0], second[idx2][0]),
min(first[idx1][1], second[idx2][1])}));
if (first[idx1][1] > second[idx2][1]) {
++idx2;
} else {
++idx1;
}
}
}
return ans;
}
// 1272. Remove Interval
// With binary search
vector<vector<int>> removeInterval(vector<vector<int>>& intervals, vector<int>& removed) {
if (intervals.front()[0] >= removed[1] || intervals.back()[1] <= removed[0])
return intervals;
auto low_it = lower_bound(intervals.begin(), intervals.end(), removed[0], [](
const vector<int>& v1, const int& num) {
return v1[1] <= num;
});
auto high_it = lower_bound(begin(intervals), end(intervals), removed[1], [](
const vector<int>& v1, const int& num) {
return v1[1] <= num;
});
const auto high_val = high_it == intervals.end() ? vector<int>() : (*high_it);
const bool same_int = low_it == high_it;
bool change_low =false;
if ((*low_it)[0] < removed[0]) {
(*low_it)[1] = removed[0];
++low_it;
change_low = true;
}
if (high_it != intervals.end()) {
if (same_int && change_low) {
intervals.insert(low_it, vector<int>({max(high_val[0], removed[1]), high_val[1]}));
} else {
(*high_it)[0] = max(high_val[0], removed[1]);
}
}
if (low_it < high_it) {
intervals.erase(low_it, high_it);
}
return intervals;
}
